스몰 월드 효과 (Small World Effect)
임의로 뽑아낸 2 사람도 6 다리만 건너면 서로 연관이 된다는 얘기가 있습니다.
이게 그냥 통설이 아니고, 사실 과학적으로 밝혀진 얘기죠. (six degrees of separation)
Six degrees of separation 은 다음과 같은 내용 입니다.
때는 1967년.
하버드 대학 심리학 교수인 스탠리 밀그램(Stanley Milgram)은 네브래스카주의 오마하에 사는 사람을 임의로 추출해서 160 통의 편지를 띄웁니다.
그 편지를 최종적으로 받는 사람은 보스톤에 사는 한 증권 브로커 였구요.
편지 내용에는 이렇게 적혀 있었습니다.
"이 편지는 보스톤 xxx에 사는 증권 브로커에게 전달되어야 할 편지 입니다. 이 증권 브로커의 이름을 참조해서, 귀하가 알고 계시는 분중 가장 이 사람에 '근접'하다고 생각되는 사람께 발송해 주시기 바랍니다"
편지는 보스톤의 그 증권 브로커를 향해 , 매번 '아는 사람에서 아는 사람으로' 방식으로 전달되어 갔습니다.
최종적으로는 그 보스톤 증권 브로커를 '아는' 사람이 마지막으로 그 편지를 발송 해줄 수 있도록 말입니다.
160통의 편지중에 최종적으로 증권 브로커에게 전달되는데 성공한 편지는 42통이었습니다.
그리고 놀랍게도 전달된 편지가 몇 사람을 거쳐서 도착했는지를 조사해 보니.
평균 5.5 명에 불과했다는 것입니다.
네브라스카에서 보스톤 까지.
딱 5.5 명만에 도착 !
이것을 "Six degrees of separation" 이라 합니다.
정말 세상이 '좁다'는 것을 최초로 실증한 실험이었죠. 주1
케빈 베이컨 이라는 헐리우드 배우가 있습니다.
아무 헐리웃 배우나 한 명 임의로 지목했을때:
그 배우가 케빈 베이컨과 같은 영화에 출현했다면 0점.
그 배우가 케빈 베이컨과 함께 영화를 찍은 다른 배우와 함께 영화를 찍었다면 1점.
이런 식으로 했을때.
놀랍게도 아무 배우나 지목하더라도 케빈 베이컨과 4점 이내에서 다 관계가 되더라는 겁니다.
그 많은 헐리우드 배우 중에서 말입니다. (심지어 챨리 채플린도 3 점에 불과 하더군요)
정말 신기하지 않습니까 ? 왜 이런 일이 생기는가.
(직접 확인해 보려면 케빈베이컨 넘버 클릭 하세요)
바로 이런것을 설명해 주는 것이 스몰-월드 효과(small-world effect) 입니다.
스몰-월드 효과는 코넬대학의 Duncan Watts, Steven Strogatz라는 두 명의 학자가 Nature지에 기고한 논문을 통해서 최초로 세상에 알려지게 됩니다.
이 효과는 위에서 말한것과 같은 '케빈 베이컨 넘버' 같은 것을 설명해 주며 굉장한 반향을 불러일으키게 되죠.
복잡한 수학을 알고 싶으시다면 논문 원문을 보셔야 하는데요. 예전엔 네이쳐지가 공개되어 있더니 이제는 유료화가 되어 버렸군요. 그 논문의 결론만 얘기하면 이런 겁니다.
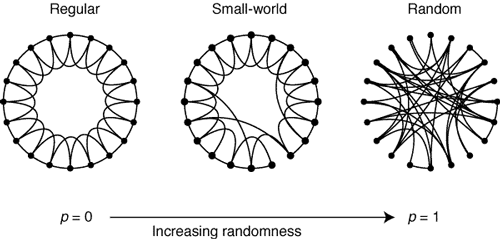
모든 네트웍은 그 연결 방식에 따라 크게 3 가지로 나눠질 수 있습니다.
일정한 규칙에 따라 인접한 곳과 일정한 숫자로만 링크되는 'regular network'이 있고 그야말로 무작위로 서로 연결되어 있는 'random network'이 있습니다.
이 둘의 중간쯤에 있는 즉 구성원의 일부만이 전혀 엉뚱한 곳으로 연결되어 있는 네트웍을 'small-world network' 이라고 합니다.
만약 어떤 집단에 감기 걸린 사람이 한 명 나타났다고 할때 그 집단이 레귤라 네트웍 이라면, 즉 모든 사람은 주변 몇 사람만 일정한 숫자로 연결되어 있는 경우와 각 구성원이 무작위로 여기 저기 연결되어 있는 경우, 어느쪽이 감기가 빨리 퍼지겠습니까? 당연히 랜덤 네트웍 쪽이겠죠?
그런데 대단히 이상하게도 엉뚱한 곳으로 연결된 구성원이 딱 몇 사람만 있는 경우에도 감기가 급속하게 퍼지는 것으로 나타나더라는 겁니다.
이것이 바로 스몰-월드 효과 때문입니다.
1학년 1반에 감기 걸린 아해가 한 명 나타났다고 합시다.
그런데 그 반 학생들이 '레귤라 네트웍' 을 이루고 있다면, 즉 다른 반 아이들과 전혀 어울리지 않는다면. 당연히 감기는 학교 전체로 퍼지지 않습니다.
만약 그 반 학생들이 '랜덤 네트웍', 즉 1반 아이들 모두가 2반, 3반, . . 9 반까지 마구 마구 어울린다면 삽시간에 감기가 전학교로 퍼지겠죠?
그런데, 그 반에 점심시간만 되면 2반 부터 9반까지를 두루 휩쓸고 다니는 친구가 딱 2-3명 정도만 있다고 해봅시다. 그리고 각 반에 그런 친구가 1-2명만 있다고 가정해 보시기 바랍니다.
이 경우에도 감기는 전 학교로 삽시간에 퍼져 버립니다.
이처럼 네트웍 자체가 굉장히 방대함에도 불구하고,알고 보면 엉뚱한 곳으로 링크되어 있는 소수의 멤버 때문에 네트웍 전체가 서로 서로 매우 밀접한 관계에 놓인것처럼 되는 걸 '스몰-월드 효과' 라고 합니다.
문자그대로 '좁은 세상' 효과 인것이죠.
이해를 돕기 위해 논문에 있는 그래프를 보여 드리겠습니다.
위 그림에서 p는 어떤 네트웍이 '무작위로 링크될' 확률을 나타냅니다. 따라서 p=0 인 경우는 레귤라 네트웍, p=1 인 경우는 랜덤 네트웍이 되겠죠.
또, clustering과 path length 라는 개념이 있습니다.
클러스터링은 '얼마나 덩어리 지워지느냐'는 것을 뜻합니다. a가 b를 알고, b가 c를 아는데 a도 c를 안다면 클러스터링 정도가 큰 것입니다. 패쓰 길이 란 것은 한 꼭지점에서 다른 꼭지점 까지 가는데 몇 단계를 거쳐서 가야 하느냐를 뜻합니다.
레귤라 네트웍 처럼 링크가 일정 숫자에 일정 패턴으로만 이루지는 경우는 당연히 한 덩어리로 묶을 수 있는 부분이 많아집니다. 클러스터링 정도가 커지겠죠. 하지만 한 꼭지점에서 다른 꼭지점으로 가는것은 항상 일정한 간격을 거쳐가야 하기 때문에 한쪽 끝에서 한쪽 끝까지의 패쓰 길이는 길어 집니다. 반면, 랜덤 네트웍의 경우엔 클러스터링 정도는 작습니다. 무작위로 얽혀있기 때문에 일정하게 그룹 짓기가 힘듭니다. 그러나 패쓰 길이는 매우 줄어듭니다. 한 꼭지점에서 다른 꼭지점으로 건너갈 경우의 수가 많아지니까요.
스몰-월드 효과는, 클러스터링이 큰, 각기 덩어리 지워지는 정도가 큰 네트웍에서도 몇 개의 특이한 링크가 존재하는 경우 임의의 두 지점 간의 패쓰 길이가 훨씬 단축되는 것을 의미하는 것입니다.
스몰-월드 효과는 여러가지 현상을 아주 매력적으로 잘 설명해 주고 있습니다. 우리 신체의 신경망이 망가져서 뇌가 동작을 멈추는 것이 꼭 모든 브레인 쎌이 다 문제가 생겨서 그런것은 아니다, 오히려 한 두개의 이상한 연결을 가진 쎌이 파괴를 순식간에 넓은 범위로 퍼뜨릴 수 있다는 것등.
검색 엔진과 바이럴 마케팅 (Viral Marketing)
위에서 살펴본 스몰-월드 효과의 다른 의미를 좀 살펴보도록 합시다.
예전에 올린 글 중에 '바이럴 마케팅'이란 글이 있었습니다. 고객을 자기 회사 영업 사원으로 만들어 버리는 마케팅 입니다. 그런데 바이어럴 마케팅이 왜 그렇게 급속하게 파급되는가는 위에서 얘기한 스몰-월드 효과를 이용해서 쉽게 이해해볼 수 있습니다. 굳이 모든 사람들이 서로 서로 긴밀하게 연결 (랜덤 네트웍) 되어 있지 않더라도 네트웍 내의 어떤 한 두 멤버(보통 1%만 있어도 스몰-월드 효과가 나타난다고 합니다)가 한메일 같은 바이어럴 마케팅 제품을 순식간에 여기저기 퍼뜨리면서, 또 그렇게 '감염' 된 집단내의 또다른 한 두명이 또 다른 집단으로 퍼뜨리게 되고...이런식으로 엄청난 확산이 이뤄지게 되는 겁니다. 모든 사람들이 긴밀하게 연결되지 않은 상태라도 순식간에 여러 곳으로 급속 확산이 됩니다.
검색엔진도 스몰-월드 효과와 관계가 있습니다. 월드와이드웹이 사실상 스몰-월드 네트웍에 속하기 때문에 (=각 문서들이 서로 서로 잘 연결되어 있는건 아니지만, 중간 중간의 소수에 의해 결국 몇 다리 안건너면 찾아낼 수 있는 상태에 있기 때문에) 굳이 아주 정교한 검색엔진을 쓰지 않더라도 조금만 시간을 들이면 원하는 문서로 도달할 수 있다는 것입니다.이것을 증명해 놓은 논문을 제록스 PARC 연구원이 발표했습니다.
논문 내용을 보면. 어떤 주제를 갖고 검색해보면 항상 '센터' 격이 싸이트가 있어서 굳이 검색엔진에서 이 센터 싸이트를 찾지 못하더라도, 다른 싸이트 대부분이 이 '센터 싸이트' 로의 링크를 마련해 놓았기 때문에 그 싸이트를 통해 몇 단계 내에서 원하는 문서를 찾아낼 수 있다는 얘기가 나옵니다. 이러한 '센터'에 해당하는 대형 싸이트들이 몇개만 항상 나타나게 된다는 것이 Power-law 분포에 의해 잘 설명되어 있기도 하구요.또 이러한 상호 링크 정도를 통해서 그 커뮤니티의 결속정도를 알 수 있다는 얘기도 있습니다. 여기서 커뮤니티는 우리가 일반적으로 생각하는 그런 커뮤니티는 아닙니다.네이버나 야후! 같은 검색엔진에서 어떤 검색어를 치고 나면 '결과' 페이지가 뜨지 않습니까? 그 결과 페이지에 떠오른 모든 링크는 사실상 그 검색어를 중심으로 구성된 하나의 커뮤니티인 것입니다.
인공유산에 찬성 하는 쪽(abortion pro-choice)과 반대 하는쪽(abortion pro-life)이 있을때 검색엔진에서 이들 각각을 검색 해보면 pro-choice쪽은 각 싸이트들 끼리의 링크가 많지 않다고 합니다. 역으로 pro-life쪽은 서로 서로 긴밀하게 링크가 되어 있습니다.. 이를 통해서 인공유산에 반대하는쪽이 보다 더 결속력이 강한 '커뮤니티'를 이루고 있음을 알 수 있는 것입니다.
따라서, 광고를 한다면 위와 같이 간접적인 방식으로 그 커뮤니티의 결속력을 확인해봐서 가급적 결속력이 좋은 커뮤니티를 택해서 광고를 하는 것이 더 유리하다는 것이죠.
스몰-월드 효과, 재밌지 않습니까?
알고보면 우린 좁은 세상에 사는 겁니다.
주1 한편, 스탠리 밀그램 교수의 '좁은 세상' 효과에 대한 반박이 최근들어 발표되고 있습니다. 대표적인 반박 중 하나인 클라인펠드 (앨러스카 패어뱅스 대학 심리학 교수) 의 주장은 이렇습니다.
첫째, 밀그램 교수의 그 실험 자체가 많은 편향성을 갖고 있다는 것입니다. 밀그램은, 처음 우편물을 발송하는 네브라스카주의 사람들을 선택할때 블루칩 주식을 다수 보유한 재산이 많은 사람들을 상당수 택했다는 것입니다. 이는 곧 보스톤에 사는 증권 브로커와 아무래도 어떤 '연결'이 있을 가능성을 높여줄 수 있는 것이구요. 게다가, 그렇지 않은 경우에도 무작위 선택이 아닌, '인맥이 풍부한 분을 구합니다'라는 신문광고를 통해서 이뤄졌고 일부는 메일링 리스트를 통해 구입한 주소와 이름을 사용했다는 것입니다. 따라서, 이후 많이 쏟아져나온 무작위 선택을 이용한 유사한 '좁은 세상 효과' 실증 연구가 대개 매우 낮은 도착 성공률 및 훨씬 더 큰 단계로 끝나버린 것이 밀그램 교수의 오리지널 연구가 많은 편향성을 갖고 있기 때문이라는 것입니다.
클라인펠드 교수는 한 발 더 나아가서, 오히려 우리의 '연결'이 인종이나 副의 장벽에 가려져 있다는 것이 후속 실험이나 자신의 추가적인 연구에서 드러났다고 얘기 합니다. 똑같은 실험을 하더라도 최종 수령인이 백인인 경우와 흑인인 경우에 있어 성공률이 몇 배 이상 차이가 나고 있고, 특징적으로 수입이 높은 사람은 수입 여부와 관계 없이 다양하고 풍부한 연결을 갖고 있음에 반해 수입이 낮은 사람은 그런 네트웍에서 소외가 되어 있더라는 겁니다. 즉, 사회적으로 성공하고 경제적으로 풍요로운 사람일수록 더 많은 '연결'을 소유하고 있는 것이지 무작위로 선택할때 몇 단계만 건너면 만난다는 신화는 허구라는 것이죠. 저소득자 -> 고소득자로의 연결은 있는지 몰라도 고소득자->저소득자로의 연결은 훨씬 더 취약하다는 것입니다.
그리고 후속 연구들을 살펴보면, 한 도시 내부나, 동일 빌딩등에서 이뤄진 연구들은 많지만 두 도시 이상을 포함하는 연구는 거의 없다라는 것 역시 밀그램 교수의 주장의 설득력을 떨어뜨리고 있답니다. 밀그램의 오리지널 연구 자체가 하나의 예외적인 것은 아니냐는 것이죠. 오히려 교수는, 사람들이 '좁은 세상 효과'를 아주 쉽게 믿는 것 자체에 어떤 심리적인 이유가 있는것 아니냐는 얘기를 합니다. 좁은 세상을 믿게 되면 그만큼 세상을 따뜻한 곳으로 인식하게 되고, 또 우연히 옛날 친구를 만나게 되면 그 인상이 깊게 오래 간다는 점등이 사람들로 하여금 '6단계만 건너면 다 아는 사이'라는 신화를 믿게 만든다는 것이죠.
뭐가 진실일까요. 어쨌든 생각한것보다는 훨씬 세상이 좁은 것인것만은 부인하기 힘들 겁니다. 만약 우리나라에서 비슷한 실험을 하면 더욱 놀라운 결과가 나올 것이라고 생각합니다. 인종적 장벽도 없고, '연'을 유난히 중시하는 우리나라는 확실히 좁은 세상일 겁니다.
-웹비즈, 이명현
'사 > ㅡ' 카테고리의 다른 글
| 스티브 잡스, 7가지 혁신의 비밀 (0) | 2010.10.11 |
|---|---|
| 스나이퍼 (0) | 2008.01.17 |
| 스티브 잡스 (0) | 2007.02.20 |
| 스티븐 킹 Stephen King, 그는 소설의 신 아닐까? (0) | 2007.01.01 |
| 스타워즈 한국순회전: 061219 (0) | 2006.12.30 |
| 스머프에 얽힌 음모이론, 그 열 가지 증거 (0) | 2002.07.10 |
| 스머프smurf -개구장이 스머프는 공산주의자였다! (0) | 2001.11.16 |
| 스푸트니크 1호 (0) | 2001.10.22 |
| 스티븐 호킹. 현대판 갈릴레오. (0) | 2001.10.16 |
| 스펜서 튜닉 Spencer Tunick (0) | 2001.10.10 |